（博主亲自录制视频）

ttps://www.zhihu.com/question/28641663

作者：城东

链接：https://www.zhihu.com/question/28641663/answer/110165221

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

目录

1 特征工程是什么？
2 数据预处理
　　2.1 无量纲化
　　　　2.1.1 标准化
　　　　2.1.2 区间缩放法
　　　　2.1.3 标准化与归一化的区别
　　2.2 对定量特征二值化
　　2.3 对定性特征哑编码
　　2.4 缺失值计算
　　2.5 数据变换
3 特征选择
　　3.1 Filter
　　　　3.1.1 方差选择法
　　　　3.1.2 相关系数法
　　　　3.1.3 卡方检验
　　　　3.1.4 互信息法
　　3.2 Wrapper
　　　　3.2.1 递归特征消除法
　　3.3 Embedded
　　　　3.3.1 基于惩罚项的特征选择法
　　　　3.3.2 基于树模型的特征选择法
4 降维
　　4.1 主成分分析法（PCA）
　　4.2 线性判别分析法（LDA）
5 总结
6 参考资料

1 特征工程是什么？

　　有这么一句话在业界广泛流传：数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已。那特征工程到底是什么呢？顾名思义，其本质是一项工程活动，目的是最大限度地从原始数据中提取特征以供算法和模型使用。通过总结和归纳，人们认为特征工程包括以下方面：

<img src="https://pic1.zhimg.com/50/20e4522e6104ad71fc543cc21f402b36_hd.jpg" data-rawwidth="875" data-rawheight="967" class="origin_image zh-lightbox-thumb" width="875" data-original="https://pic1.zhimg.com/20e4522e6104ad71fc543cc21f402b36_r.jpg">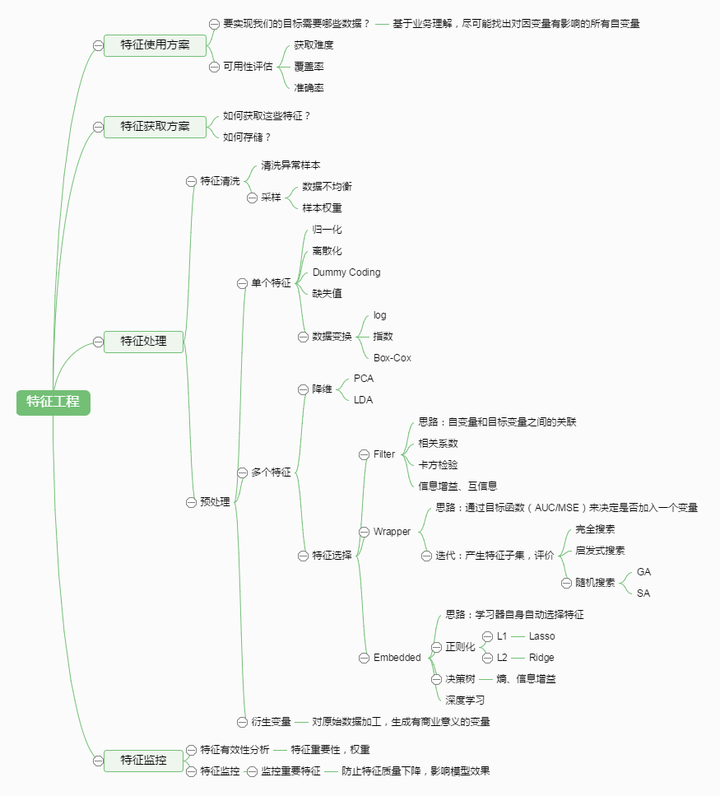

　　特征处理是特征工程的核心部分，sklearn提供了较为完整的特征处理方法，包括数据预处理，特征选择，降维等。首次接触到sklearn，通常会被其丰富且方便的算法模型库吸引，但是这里介绍的特征处理库也十分强大！

　　本文中使用sklearn中的来对特征处理功能进行说明。IRIS数据集由Fisher在1936年整理，包含4个特征（Sepal.Length（花萼长度）、Sepal.Width（花萼宽度）、Petal.Length（花瓣长度）、Petal.Width（花瓣宽度）），特征值都为正浮点数，单位为厘米。目标值为鸢尾花的分类（Iris Setosa（山鸢尾）、Iris Versicolour（杂色鸢尾），Iris Virginica（维吉尼亚鸢尾））。导入IRIS数据集的代码如下：

from sklearn.datasets import load_iris #导入IRIS数据集 iris = load_iris() #特征矩阵 iris.data #目标向量 iris.target

2 数据预处理

　　通过特征提取，我们能得到未经处理的特征，这时的特征可能有以下问题：

• 不属于同一量纲：即特征的规格不一样，不能够放在一起比较。无量纲化可以解决这一问题。
• 信息冗余：对于某些定量特征，其包含的有效信息为区间划分，例如学习成绩，假若只关心“及格”或不“及格”，那么需要将定量的考分，转换成“1”和“0”表示及格和未及格。二值化可以解决这一问题。
• 定性特征不能直接使用：某些机器学习算法和模型只能接受定量特征的输入，那么需要将定性特征转换为定量特征。最简单的方式是为每一种定性值指定一个定量值，但是这种方式过于灵活，增加了调参的工作。：假设有N种定性值，则将这一个特征扩展为N种特征，当原始特征值为第i种定性值时，第i个扩展特征赋值为1，其他扩展特征赋值为0。哑编码的方式相比直接指定的方式，不用增加调参的工作，对于线性模型来说，使用哑编码后的特征可达到非线性的效果。
• 存在缺失值：缺失值需要补充。
• 信息利用率低：不同的机器学习算法和模型对数据中信息的利用是不同的，之前提到在线性模型中，使用对定性特征哑编码可以达到非线性的效果。类似地，对定量变量多项式化，或者进行其他的转换，都能达到非线性的效果。

　　我们使用sklearn中的preproccessing库来进行数据预处理，可以覆盖以上问题的解决方案。

2.1 无量纲化

　　无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化和区间缩放法。标准化的前提是特征值服从正态分布，标准化后，其转换成标准正态分布。区间缩放法利用了边界值信息，将特征的取值区间缩放到某个特点的范围，例如[0, 1]等。

2.1.1 标准化

　　标准化需要计算特征的均值和标准差，公式表达为：

　　使用preproccessing库的StandardScaler类对数据进行标准化的代码如下：

<img src="https://pic1.zhimg.com/50/c7e852db6bd05b7bb1017b5425ffeec1_hd.jpg" data-rawwidth="81" data-rawheight="48" class="content_image" width="81">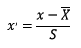

from sklearn.preprocessing import StandardScaler #标准化，返回值为标准化后的数据 StandardScaler().fit_transform(iris.data)

2.1.2 区间缩放法

　　区间缩放法的思路有多种，常见的一种为利用两个最值进行缩放，公式表达为：

　　使用preproccessing库的MinMaxScaler类对数据进行区间缩放的代码如下：

<img src="https://pic1.zhimg.com/50/0f119a8e8f69509c5b95ef6a8a01a809_hd.jpg" data-rawwidth="119" data-rawheight="52" class="content_image" width="119">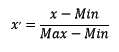

from sklearn.preprocessing import MinMaxScaler#区间缩放，返回值为缩放到[0, 1]区间的数据MinMaxScaler().fit_transform(iris.data)

2.1.3 标准化与归一化的区别

　　简单来说，标准化是依照特征矩阵的列处理数据，其通过求z-score的方法，将样本的特征值转换到同一量纲下。归一化是依照特征矩阵的行处理数据，其目的在于样本向量在点乘运算或其他核函数计算相似性时，拥有统一的标准，也就是说都转化为“单位向量”。规则为l2的归一化公式如下：

<img src="https://pic4.zhimg.com/50/fbb2fd0a163f2fa211829b735194baac_hd.jpg" data-rawwidth="113" data-rawheight="57" class="content_image" width="113">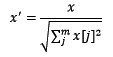

　　使用preproccessing库的Normalizer类对数据进行归一化的代码如下：

from sklearn.preprocessing import Normalizer #归一化，返回值为归一化后的数据 Normalizer().fit_transform(iris.data)

2.2 对定量特征二值化

　　定量特征二值化的核心在于设定一个阈值，大于阈值的赋值为1，小于等于阈值的赋值为0，公式表达如下：

<img src="https://pic3.zhimg.com/50/11111244c5b69c1af6c034496a2591ad_hd.jpg" data-rawwidth="159" data-rawheight="41" class="content_image" width="159">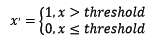

　　使用preproccessing库的Binarizer类对数据进行二值化的代码如下：

from sklearn.preprocessing import Binarizer #二值化，阈值设置为3，返回值为二值化后的数据 Binarizer(threshold=3).fit_transform(iris.data)

2.3 对定性特征哑编码

　　由于IRIS数据集的特征皆为定量特征，故使用其目标值进行哑编码（实际上是不需要的）。使用preproccessing库的OneHotEncoder类对数据进行哑编码的代码如下：

from sklearn.preprocessing import OneHotEncoder #哑编码，对IRIS数据集的目标值，返回值为哑编码后的数据 OneHotEncoder().fit_transform(iris.target.reshape((-1,1)))

2.4 缺失值计算

　　由于IRIS数据集没有缺失值，故对数据集新增一个样本，4个特征均赋值为NaN，表示数据缺失。使用preproccessing库的Imputer类对数据进行缺失值计算的代码如下：

from numpy import vstack, array, nan from sklearn.preprocessing import Imputer #缺失值计算，返回值为计算缺失值后的数据 #参数missing_value为缺失值的表示形式，默认为NaN #参数strategy为缺失值填充方式，默认为mean（均值） Imputer().fit_transform(vstack((array([nan, nan, nan, nan]), iris.data)))

2.5 数据变换

　　常见的数据变换有基于多项式的、基于指数函数的、基于对数函数的。4个特征，度为2的多项式转换公式如下：

<img src="https://pic1.zhimg.com/50/d1c57a66fad39df90b87cea330efb3f3_hd.jpg" data-rawwidth="571" data-rawheight="57" class="origin_image zh-lightbox-thumb" width="571" data-original="https://pic1.zhimg.com/d1c57a66fad39df90b87cea330efb3f3_r.jpg">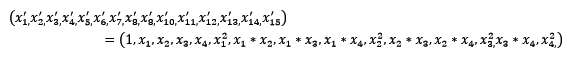

　　使用preproccessing库的PolynomialFeatures类对数据进行多项式转换的代码如下：

from sklearn.preprocessing import PolynomialFeatures #多项式转换 #参数degree为度，默认值为2 PolynomialFeatures().fit_transform(iris.data)

　　基于单变元函数的数据变换可以使用一个统一的方式完成，使用preproccessing库的FunctionTransformer对数据进行对数函数转换的代码如下：

from numpy import log1p from sklearn.preprocessing import FunctionTransformer #自定义转换函数为对数函数的数据变换 #第一个参数是单变元函数 FunctionTransformer(log1p).fit_transform(iris.data)

3 特征选择

　　当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：

• 特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
• 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。

　　根据特征选择的形式又可以将特征选择方法分为3种：

• Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
• Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
• Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

　　我们使用sklearn中的feature_selection库来进行特征选择。

3.1 Filter

3.1.1 方差选择法

　　使用方差选择法，先要计算各个特征的方差，然后根据阈值，选择方差大于阈值的特征。使用feature_selection库的VarianceThreshold类来选择特征的代码如下：

from sklearn.feature_selection import VarianceThreshold #方差选择法，返回值为特征选择后的数据 #参数threshold为方差的阈值 VarianceThreshold(threshold=3).fit_transform(iris.data)

3.1.2 相关系数法

　　使用相关系数法，先要计算各个特征对目标值的相关系数以及相关系数的P值。用feature_selection库的SelectKBest类结合相关系数来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest from scipy.stats import pearsonr #选择K个最好的特征，返回选择特征后的数据 #第一个参数为计算评估特征是否好的函数，该函数输入特征矩阵和目标向量，输出二元组（评分，P值）的数组，数组第i项为第i个特征的评分和P值。在此定义为计算相关系数 #参数k为选择的特征个数 SelectKBest(lambda X, Y: array(map(lambda x:pearsonr(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

3.1.3 卡方检验

　　经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量：

<img src="https://pic2.zhimg.com/50/7bc586c806b9b8bf1e74433a2e1976bc_hd.jpg" data-rawwidth="162" data-rawheight="48" class="content_image" width="162">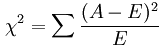

　　不难发现，。用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 #选择K个最好的特征，返回选择特征后的数据 SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)

3.1.4 互信息法

　　经典的互信息也是评价定性自变量对定性因变量的相关性的，互信息计算公式如下：

<img src="https://pic4.zhimg.com/50/6af9a077b49f587a5d149f5dc51073ba_hd.jpg" data-rawwidth="274" data-rawheight="50" class="content_image" width="274">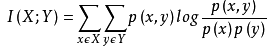

　　为了处理定量数据，最大信息系数法被提出，使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest from minepy import MINE #由于MINE的设计不是函数式的，定义mic方法将其为函数式的，返回一个二元组，二元组的第2项设置成固定的P值0.5 def mic(x, y): m = MINE() m.compute_score(x, y) return (m.mic(), 0.5) #选择K个最好的特征，返回特征选择后的数据 SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

3.2 Wrapper

3.2.1 递归特征消除法

　　递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，消除若干权值系数的特征，再基于新的特征集进行下一轮训练。使用feature_selection库的RFE类来选择特征的代码如下：

from sklearn.feature_selection import RFE from sklearn.linear_model import LogisticRegression #递归特征消除法，返回特征选择后的数据 #参数estimator为基模型 #参数n_features_to_select为选择的特征个数 RFE(estimator=LogisticRegression(), n_features_to_select=2).fit_transform(iris.data, iris.target)

3.3 Embedded

3.3.1 基于惩罚项的特征选择法

　　使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel from sklearn.linear_model import LogisticRegression #带L1惩罚项的逻辑回归作为基模型的特征选择 SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)

　　实际上，，所以没选到的特征不代表不重要。故，可结合L2惩罚项来优化。具体操作为：若一个特征在L1中的权值为1，选择在L2中权值差别不大且在L1中权值为0的特征构成同类集合，将这一集合中的特征平分L1中的权值，故需要构建一个新的逻辑回归模型：

from sklearn.linear_model import LogisticRegression class LR(LogisticRegression): def __init__(self, threshold=0.01, dual=False, tol=1e-4, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear', max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1): #权值相近的阈值 self.threshold = threshold LogisticRegression.__init__(self, penalty='l1', dual=dual, tol=tol, C=C, fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight=class_weight, random_state=random_state, solver=solver, max_iter=max_iter, multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs) #使用同样的参数创建L2逻辑回归 self.l2 = LogisticRegression(penalty='l2', dual=dual, tol=tol, C=C, fit_intercept=fit_intercept, intercept_scaling=intercept_scaling, class_weight = class_weight, random_state=random_state, solver=solver, max_iter=max_iter, multi_class=multi_class, verbose=verbose, warm_start=warm_start, n_jobs=n_jobs) def fit(self, X, y, sample_weight=None): #训练L1逻辑回归 super(LR, self).fit(X, y, sample_weight=sample_weight) self.coef_old_ = self.coef_.